转载:著名的 P=NP 问题到底是什么
Overview
这篇文章对于N和NP问题讲解的非常通俗易通,值得一读。
以下为正文
你会经常看到网上出现“这怎么做,这不是NP问题吗”、“这个只有搜了,这已经被证明是NP问题了”之类的话。这或许是众多OIer最大的误区之一。你要知道,大多数人此时所说的NP问题其实都是指的NPC问题。他们没有搞清楚NP问题和NPC问题的概念。NP问题并不是那种“只有搜才行”的问题,NPC问题才是。
好,行了,基本上这个误解已经被澄清了。下面的内容都是在讲什么是P问题,什么是NP问题,什么是NPC问题,你如果不是很感兴趣就可以不看了。接下来你可以看到,把NP问题当成是 NPC问题是一个多大的错误。
还是先用几句话简单说明一下时间复杂度。时间复杂度并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序需要的时间长度增长得有多快。
也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。
不管数据有多大,程序处理花的时间始终是那么多的,我们就说这个程序很好,具有O(1)的时间复杂度,也称常数级复杂度;数据规模变得有多大,花的时间也跟着变得有多长,这个程序的时间复杂度就是O(n),比如找n个数中的最大值;而像冒泡排序、插入排序等,数据扩大2倍,时间变慢4倍的,属于O(n^2)的复杂度。
还有一些穷举类的算法,所需时间长度成几何阶数上涨,这就是O(a^n)的指数级复杂度,甚至O(n!)的阶乘级复杂度。不会存在O(2*n^2)的复杂度,因为前面的那个“2”是系数,根本不会影响到整个程序的时间增长。同样地,O (n^3+n^2)的复杂度也就是O(n^3)的复杂度。
因此,我们会说,一个O(0.01n^3)的程序的效率比O(100n^2)的效率低,尽管在n很小的时候,前者优于后者,但后者时间随数据规模增长得慢,最终O(n^3)的复杂度将远远超过O(n^2)。我们也说,O(n^100)的复杂度小于O(1.01^n)的复杂度。
容易看出,前面的几类复杂度被分为两种级别,其中后者的复杂度无论如何都远远大于前者:一种是O(1),O(log(n)),O(n^a)等,我们把它叫做多项式级的复杂度,因为它的规模n出现在底数的位置;另一种是O(a^n)和O(n!)型复杂度,它是非多项式级的,其复杂度计算机往往不能承受。
当我们在解决一个问题时,我们选择的算法通常都需要是多项式级的复杂度,非多项式级的复杂度需要的时间太多,往往会超时,除非是数据规模非常小。
自然地,人们会想到一个问题:会不会所有的问题都可以找到复杂度为多项式级的算法呢?很遗憾,答案是否定的。有些问题甚至根本不可能找到一个正确的算法来,这称之为“不可解问题”(Undecidable Decision Problem)。
The Halting Problem就是一个著名的不可解问题,在我的Blog上有过专门的介绍和证明。再比如,输出从1到n这n个数的全排列。不管你用什么方法,你的复杂度都是阶乘级,因为你总得用阶乘级的时间打印出结果来。
有人说,这样的“问题”不是一个“正规”的问题,正规的问题是让程序解决一个问题,输出一个“YES”或“NO”(这被称为判定性问题),或者一个什么什么的最优值(这被称为最优化问题)。那么,根据这个定义,我也能举出一个不大可能会有多项式级算法的问题来:Hamilton回路。
问题是这样的:给你一个图,问你能否找到一条经过每个顶点一次且恰好一次(不遗漏也不重复)最后又走回来的路(满足这个条件的路径叫做Hamilton回路)。这个问题现在还没有找到多项式级的算法。事实上,这个问题就是我们后面要说的NPC问题。
下面引入P类问题的概念:如果一个问题可以找到一个能在多项式的时间里解决它的算法,那么这个问题就属于P问题。
****P是英文单词多项式的第一个字母。哪些问题是P类问题呢?通常NOI和NOIP不会出不属于P类问题的题目。我们常见到的一些信息奥赛的题目都是P问题。道理很简单,一个用穷举换来的非多项式级时间的超时程序不会涵盖任何有价值的算法。
接下来引入NP问题的概念。这个就有点难理解了,或者说容易理解错误。在这里强调(回到我竭力想澄清的误区上),NP问题不是非P类问题。NP问题是指可以在多项式的时间里验证一个解的问题。NP问题的另一个定义是,可以在多项式的时间里猜出一个解的问题。
比方说,我RP很好,在程序中需要枚举时,我可以一猜一个准。现在某人拿到了一个求最短路径的问题,问从起点到终点是否有一条小于100个单位长度的路线。它根据数据画好了图,但怎么也算不出来,于是来问我:你看怎么选条路走得最少?
我说,我RP很好,肯定能随便给你指条很短的路出来。然后我就胡乱画了几条线,说就这条吧。那人按我指的这条把权值加起来一看,嘿,神了,路径长度98,比100小。于是答案出来了,存在比100小的路径。别人会问他这题怎么做出来的,他就可以说,因为我找到了一个比100 小的解。
在这个题中,找一个解很困难,但验证一个解很容易。验证一个解只需要O(n)的时间复杂度,也就是说我可以花O(n)的时间把我猜的路径的长度加出来。那么,只要我RP好,猜得准,我一定能在多项式的时间里解决这个问题。我猜到的方案总是最优的,不满足题意的方案也不会来骗我去选它。这就是NP问题。
当然有不是NP问题的问题,即你猜到了解但是没用,因为你不能在多项式的时间里去验证它。下面我要举的例子是一个经典的例子,它指出了一个目前还没有办法在多项式的时间里验证一个解的问题。
很显然,前面所说的Hamilton回路是NP问题,因为验证一条路是否恰好经过了每一个顶点非常容易。但我要把问题换成这样:试问一个图中是否不存在Hamilton回路。这样问题就没法在多项式的时间里进行验证了,因为除非你试过所有的路,否则你不敢断定它“没有Hamilton回路”。
之所以要定义NP问题,是因为通常只有NP问题才可能找到多项式的算法。我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。相信读者很快明白,信息学中的号称最困难的问题——“NP问题”,实际上是在探讨NP问题与P类问题的关系。
很显然,所有的P类问题都是NP问题。也就是说,能多项式地解决一个问题,必然能多项式地验证一个问题的解——既然正解都出来了,验证任意给定的解也只需要比较一下就可以了。关键是,人们想知道,是否所有的NP问题都是P类问题。
我们可以再用集合的观点来说明。如果把所有P类问题归为一个集合P中,把所有 NP问题划进另一个集合NP中,那么,显然有P属于NP。现在,所有对NP问题的研究都集中在一个问题上,即究竟是否有P=NP?通常所谓的“NP问题”,其实就一句话:证明或推翻P=NP。
NP问题一直都是信息学的巅峰。巅峰,意即很引人注目但难以解决。在信息学研究中,这是一个耗费了很多时间和精力也没有解决的终极问题,好比物理学中的大统一和数学中的歌德巴赫猜想等。
目前为止这个问题还“啃不动”。但是,一个总的趋势、一个大方向是有的。人们普遍认为,P=NP不成立,也就是说,多数人相信,存在至少一个不可能有多项式级复杂度的算法的NP问题。
人们如此坚信P≠NP是有原因的,就是在研究NP问题的过程中找出了一类非常特殊的NP问题叫做NP-完全问题,也即所谓的 NPC问题。C是英文单词“完全”的第一个字母。正是NPC问题的存在,使人们相信P≠NP。下文将花大量篇幅介绍NPC问题,你从中可以体会到NPC问题使P=NP变得多么不可思议。
为了说明NPC问题,我们先引入一个概念——约化(Reducibility,有的资料上叫“归约”)。
简单地说,一个问题A可以约化为问题B的含义即是,可以用问题B的解法解决问题A,或者说,问题A可以“变成”问题B。
《算法导论》上举了这么一个例子。比如说,现在有两个问题:求解一个一元一次方程和求解一个一元二次方程。那么我们说,前者可以约化为后者,意即知道如何解一个一元二次方程那么一定能解出一元一次方程。
我们可以写出两个程序分别对应两个问题,那么我们能找到一个“规则”,按照这个规则把解一元一次方程程序的输入数据变一下,用在解一元二次方程的程序上,两个程序总能得到一样的结果。这个规则即是:两个方程的对应项系数不变,一元二次方程的二次项系数为0。按照这个规则把前一个问题转换成后一个问题,两个问题就等价了。
同样地,我们可以说,Hamilton回路可以约化为TSP问题(Travelling Salesman Problem,旅行商问题):在Hamilton回路问题中,两点相连即这两点距离为0,两点不直接相连则令其距离为1,于是问题转化为在TSP问题中,是否存在一条长为0的路径。Hamilton回路存在当且仅当TSP问题中存在长为0的回路。
“问题A可约化为问题B”有一个重要的直观意义:B的时间复杂度高于或者等于A的时间复杂度。也就是说,问题A不比问题B难。这很容易理解。既然问题A能用问题B来解决,倘若B的时间复杂度比A的时间复杂度还低了,那A的算法就可以改进为B的算法,两者的时间复杂度还是相同。正如解一元二次方程比解一元一次方程难,因为解决前者的方法可以用来解决后者。
很显然,约化具有一项重要的性质:约化具有传递性。如果问题A可约化为问题B,问题B可约化为问题C,则问题A一定可约化为问题C。这个道理非常简单,就不必阐述了。
现在再来说一下约化的标准概念就不难理解了:如果能找到这样一个变化法则,对任意一个程序A的输入,都能按这个法则变换成程序B的输入,使两程序的输出相同,那么我们说,问题A可约化为问题B。
当然,我们所说的“可约化”是指的可“多项式地”约化(Polynomial-time Reducible),即变换输入的方法是能在多项式的时间里完成的。约化的过程只有用多项式的时间完成才有意义。
好了,从约化的定义中我们看到,一个问题约化为另一个问题,时间复杂度增加了,问题的应用范围也增大了。通过对某些问题的不断约化,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。
再回想前面讲的P和NP问题,联想起约化的传递性,自然地,我们会想问,如果不断地约化上去,不断找到能“通吃”若干小NP问题的一个稍复杂的大NP问题,那么最后是否有可能找到一个时间复杂度最高,并且能“通吃”所有的 NP问题的这样一个超级NP问题?
答案居然是肯定的。也就是说,存在这样一个NP问题,所有的NP问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的NP问题都解决了。
这种问题的存在难以置信,并且更加不可思议的是,这种问题不只一个,它有很多个,它是一类问题。这一类问题就是传说中的NPC 问题,也就是NP-完全问题。NPC问题的出现使整个NP问题的研究得到了飞跃式的发展。我们有理由相信,NPC问题是最复杂的问题。
再次回到全文开头,我们可以看到,人们想表达一个问题不存在多项式的高效算法时应该说它“属于NPC问题”。此时,我的目的终于达到了,我已经把NP问题和NPC问题区别开了。
到此为止,本文已经写了近5000字了,我佩服你还能看到这里来,同时也佩服一下自己能写到这里来。
NPC问题的定义非常简单。同时满足下面两个条件的问题就是NPC问题。首先,它得是一个NP问题;然后,所有的NP问题都可以约化到它。证明一个问题是 NPC问题也很简单。先证明它至少是一个NP问题,再证明其中一个已知的NPC问题能约化到它(由约化的传递性,则NPC问题定义的第二条也得以满足;至于第一个NPC问题是怎么来的,下文将介绍),这样就可以说它是NPC问题了。
既然所有的NP问题都能约化成NPC问题,那么只要任意一个NPC问题找到了一个多项式的算法,那么所有的NP问题都能用这个算法解决了,NP也就等于P 了。因此,给NPC找一个多项式算法太不可思议了。因此,前文才说,“正是NPC问题的存在,使人们相信P≠NP”。我们可以就此直观地理解,NPC问题目前没有多项式的有效算法,只能用指数级甚至阶乘级复杂度的搜索。
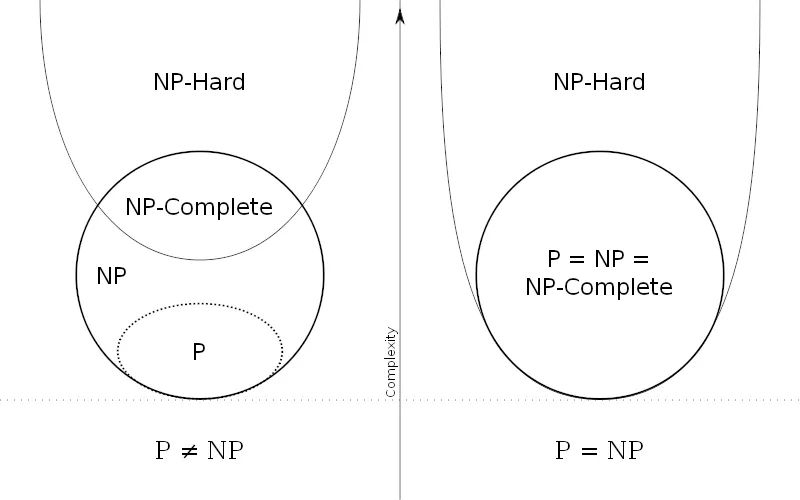
顺便讲一下NP-Hard问题。NP-Hard问题是这样一种问题,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广)。NP-Hard问题同样难以找到多项式的算法,但它不列入我们的研究范围,因为它不一定是NP问题。
即使NPC问题发现了多项式级的算法,NP-Hard问题有可能仍然无法得到多项式级的算法。事实上,由于NP-Hard放宽了限定条件,它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。
不要以为NPC问题是一纸空谈。NPC问题是存在的。确实有这么一个非常具体的问题属于NPC问题。下文即将介绍它。
下文即将介绍逻辑电路问题。这是第一个NPC问题。其它的NPC问题都是由这个问题约化而来的。因此,逻辑电路问题是NPC类问题的“鼻祖”。
逻辑电路问题是指的这样一个问题:给定一个逻辑电路,问是否存在一种输入使输出为True。
什么叫做逻辑电路呢?一个逻辑电路由若干个输入,一个输出,若干“逻辑门”和密密麻麻的线组成。看下面一例,不需要解释你马上就明白了。
┌─────┐
│输入1 |─→┐ ┌────┐
└─────┘ └─→┤ │
│ OR ├──→─┐
┌─────┐ ┌─→┤ │ │ ┌─────┐
│输入2 ├─→┤ └────┘ └→──┤ │
└─────┘ │ ┌─→─────┤ AND ├──→输出
└────────┘ ┌→─┤ │
┌─────┐ ┌─────┐ │ └─────┘
│输入3 ├──→─┤ NOT ├─→───┘
└─────┘ └────—┘
这是个较简单的逻辑电路,当输入1、输入2、输入3分别为True、True、False或False、True、False时,输出为True。
有输出无论如何都不可能为True的逻辑电路吗?有。下面就是一个简单的例子。
┌─────┐
│输入1 ├→─┐ ┌─────┐
└─────┘ └─→┤ │
│ AND ├─→──┐
┌─→┤ │ │
│ └─────┘ │ ┌─────┐
│ └→┤ │
┌─────┐ │ │ AND ├─→输出
│输入2 ├→─┤ ┌─────┐ ┌→─┤ │
└─────┘ └→─┤ NOT ├─→─┘ └─────┘
└─────┘
上面这个逻辑电路中,无论输入是什么,输出都是False。我们就说,这个逻辑电路不存在使输出为True的一组输入。
回到上文,给定一个逻辑电路,问是否存在一种输入使输出为True,这即逻辑电路问题。
逻辑电路问题属于NPC问题。这是有严格证明的。它显然属于NP问题,并且可以直接证明所有的NP问题都可以约化到它(不要以为NP问题有无穷多个将给证明造成不可逾越的困难)。
证明过程相当复杂,其大概意思是说任意一个NP问题的输入和输出都可以转换成逻辑电路的输入和输出(想想计算机内部也不过是一些 0和1的运算),因此对于一个NP问题来说,问题转化为了求出满足结果为True的一个输入(即一个可行解)。
有了第一个NPC问题后,一大堆NPC问题就出现了,因为再证明一个新的NPC问题只需要将一个已知的NPC问题约化到它就行了。后来,Hamilton 回路成了NPC问题,TSP问题也成了NPC问题。现在被证明是NPC问题的有很多,任何一个找到了多项式算法的话所有的NP问题都可以完美解决了。因此说,正是因为NPC问题的存在,P=NP变得难以置信。
P=NP问题还有许多有趣的东西,有待大家自己进一步的挖掘。攀登这个信息学的巅峰是我们这一代的终极目标。现在我们需要做的,至少是不要把概念弄混淆了。
来源:http://www.matrix67.com/blog/archives/7084#more-7084
2006 年,我在博客(当时还是 MSN Space)上发了 《什么是 P 问题、NP 问题和 NPC 问题》 一文。这是我高二搞信息学竞赛时随手写的一些东西,是我的博客中最早的文章之一。今天偶然发现,这篇现在看了恨不得重写一遍的“科普”竟仍然有比较大的阅读量。时间过得很快。《星际争霸》(StarCraft)出了续作,德国队 7 比 1 大胜东道主巴西,《学徒》(The Apprentice)里的那个家伙当了总统,非典之后竟然出了更大的疫情。现在已经是 2022 年了。这 16 年的时间里,我读了大学,出了书,娶了老婆,养了娃。如果现在的我写一篇同样话题的科普文章,我会写成什么样呢?正好,我的新书《神机妙算:一本关于算法的闲书》中有一些相关的内容。我从书里的不同章节中摘选了一些片段,整理加工了一下,弄出了下面这篇文章,或许能回答刚才的问题吧。
有一天,我和老婆去超市大采购。和往常一样,结完账之后,我们需要小心谨慎地规划把东西放进购物袋的顺序,防止东西被压坏。这并不是一件容易的事情,尤其是考虑到各个物体自身的重量和它能承受的重量之间并无必然联系。鸡蛋、牛奶非常重,但同时也很怕压;毛巾、卫生纸都很轻,但却能承受很大的压力。
于是,我突然想到了这么一个问题:给定 n 个物体各自的重量和它能承受的最大重量,判断出能否把它们叠成一摞,使得所有的物体都不会被压坏(一个物体不会被压坏的意思就是,它上面的物体的总重小于等于自己能承受的最大重量)。
事实证明,这是一个非常有趣的问题——老婆听完这个问题后整日茶饭不思,晚上做梦都在念叨着自己构造的测试数据。这里,我们不妨给出一组数据供大家玩玩。
假设有 A、B、C、D 四个物体,其中:物体 A 的自重为 1,最大承重为 9;物体 B 的自重为 5,最大承重为 2;物体 C 的自重为 2,最大承重为 4;物体 D 的自重为 3,最大载重为 12。在这个例子中,安全的叠放方式是唯一的,你能找出来吗?
答案:C 在最上面,其次是 B,其次是 A,最下面是 D。注意,在这个最优方案中,最上面的物体既不是自身重量最小的,也不是承重极限最小的,而是自身重量与承重极限之和最小的。事实上,最优方案中的四个物体就是按照这个和的大小排列的!对于某种叠放方案中的某一个物体,不妨把它的最大载重减去实际载重的结果叫作它的安全系数。
我们可以证明,这种按自身重量与载重能力之和排序的叠放策略可以让最危险的物体尽可能安全,也就是让最小的那个安全系数达到最大。如果此时所有物体的安全系数都是非负数,那么我们就相当于有了一种满足要求的叠放方案;如果此时仍然存在负的安全系数,那么我们就永远找不到让所有物体都安全的叠放方案了。
假设在某种叠放方案中,有两个相邻的物体,上面那个物体的自身重量和最大载重分别为 W1 和 P1,下面那个物体的自身重量和最大载重分别为 W2 和 P2。再假设它俩之上的所有物体的重量之和是 W,这是这两个物体都要承担的重量。
如果 W1 + P1 大于 W2 + P2,那么把这两个物体的位置交换一下,会发生什么事情呢?原先下面那个物体的安全系数为 P2 − W − W1,移到上面去之后安全系数变成了 P2 − W,这无疑使它更安全了。原先上面那个物体的安全系数为 P1 − W,移到下面后安全系数变成了 P1 − W − W2,这个值虽然减小了,但却仍然大于原先另一个物体的安全系数 P2 − W − W1(这里用到了 W1 + P1 > W2 + P2 的假设)。因此,交换两个物体之后,不但不会刷新安全系数的下限,相反有时还能向上改进它。
所以说,我们可以不断地把自身重量与载重能力之和更小的物体换到上面去,反正这不会让情况变得更糟。最终得到的最优方案,也就与我们前面给出的结论一致了。
为了解决某类问题,我们经常需要给出一个策略,或者说一个方案,或者说一个处理过程,或者说一系列操作规则,或者更贴切的,一套计算方法。这就是所谓的“算法” (algorithm)。
让我们来总结一下。我们的问题是:给定 n 个物体各自的重量,以及每个物体最大可以承受的重量,判断出能否把它们叠成一摞,使得所有的物体都不会被压坏。它的算法则是:按照自身重量与最大承重之和进行排序,然后检验这是否能让所有物体都不被压坏,它的答案就决定了整个问题的答案。有了算法后,实际的计算过程一般就会交给计算机来完成的。程序员的工作,就是编写代码,把算法告诉计算机。
让计算机把每个物体的自身重量和最大承重加起来,这好办。如果有 n 个物体,那就要算 n 遍加法。给它们排序的时候,我们要依次做下面这些事情:
- 把 n 个数逐一过一遍,找出最小的那个数(n 次操作)
- 把最小的那个数放到第 1 个位置(1 次操作)
- 把剩下的 n − 1 个数逐一过一遍,找出最小的那个数(n − 1 次操作)
- 把最小的那个数放到第 2 个位置(1 次操作)
- ……
这要用 n + 1 + (n − 1) + 1 + … + 1 + 1 = (n2 + 3n) / 2 次操作。物体从上到下该怎么摆,现在就知道了。为了检验有没有东西被压坏,则需要把物体的重量从上到下累加一遍,边加边要和下一个物体的承重做比较。
考虑到最上面的物体不用做检验,操作次数姑且就算 2(n − 1) 吧。这样的话,整个算法需要 (n2 + 9n) / 2 − 2 次操作。当然,在编写程序时,一些细节处可能还需要很多额外的操作。不过,对于运算速度极快的计算机来说,这都可以忽略不计。
计算机动辄处理成千上万的数据,多那么一两次操作不会从根本上影响整个处理过程的开销。为了评估处理数据的效率,我们更应该关注总操作次数的“级别”。我们甚至可以把 (n2 + 3n) / 2 次操作、(n2 + 9n) / 2 − 2 次操作以及 2n2 + n + 1 次操作、10n2 − 13n + 500 次操作等等,统统都叫作“操作次数以 n2 的级别增长”,它们都代表着同一个意思:当 n 很大的时候,如果 n 变成了原来的 k 倍,那么总的开销大致就会变成原来的 k2 倍。
1894 年,德国数学家保罗·巴赫曼(Paul Bachmann)提出了一种使用起来非常方便的“大 O 记号”(big O notation),用到这里真是再适合不过了。如果某个函数 f(n) 的增长速度不超过 n2 的级别,那么我们就可以记下 f(n) = O(n2)。因而,随着 n 的增加,(n2 + 3n) / 2 、(n2 + 9n) / 2 − 2 、2n2 + n + 1 、10n2 − 13n + 500 的增长速度都可以用 O(n2) 来表示。类似地,n3 / 10、(n3 + 3n) / 2、10n3 − 6n2 + 100 则都相当于 O(n3)。
完成刚才那个算法需要的操作次数是 O(n2) 级别的。假设每次操作耗时相同,那么运行这个算法所需要的时间也应该是 O(n2) 级别的。更专业的说法则是,整个算法的“时间复杂度”(time complexity)为 O(n2)。
1985 年由英特尔公司推出的 80386 芯片每秒钟可以执行 200 万个指令,1999 年的英特尔奔腾 III 处理器每秒钟可以执行 20 亿个指令,2012 年的英特尔酷睿 i7 处理器每秒则可以执行 1000 亿个以上的指令。
不妨假设,当 n = 10 的时候,借助上述算法,计算机只需要 0.1 毫秒就能得到答案。算法的时间复杂度为 O(n2),说明当 n 增加到原来的 100 倍时,运行完成所需的时间会增加到原来的 10000 倍。因此,如果 n 变成了 1000 时,计算机也只需要 1 秒就能得到答案。即使 n 增加到了 100000,计算机也只需要 10000 秒就能得到答案,这大约相当于 2 个小时又 47 分钟。
其实,为了判断出这些物体能否安全叠放,我们似乎完全不必如此煞费心机。我们还有一个更基本的方法:枚举所有可能的叠放顺序,看看有没有满足要求的方案。n 个物体一共会产生 n! 种不同的叠放顺序,每次检验都需要耗费 O(n) 的时间。所以,为了得到答案,最坏情况下的时间复杂度为 O(n · n!)。
那么,我们为什么不采用这种粗暴豪爽的算法呢?主要原因大概就是,这种算法的时间复杂度有些太高。但是,既然计算机的运算速度如此之快,O(n · n!) 的时间复杂度想必也不在话下吧?让我们来看一看。仍然假设 n = 10 的时候,计算机只需要 0.1 毫秒就能得到答案。
令人吃惊的是,若真的以 O(n · n!) 的级别增长,到了 n = 15 的时候,完成算法全过程需要的时间就已经增加到了 54 秒。当 n = 20 时,算法全过程耗时 1.34 亿秒,这相当于 1551 天,也就是 4.25 年。当 n = 30 时,算法全过程耗时 700 万亿年,而目前的资料显示,宇宙大爆炸也不过是在 137 亿年以前。
如果 n = 100 的话,计算机需要不分昼夜地工作 8.15 × 10140 年才能得到答案。根据目前的宇宙学理论,到了那个时候,整个宇宙早已一片死寂。
为什么 O(n2) 和 O(n · n!) 的差异那么大呢?原因就是,前者毕竟属于多项式级的增长,后者则已经超过了指数级的增长。
指数级的增长真的非常可怕,虽然 n 较小的时候看上去似乎很平常,但它很快就会超出你的想象,完全处于失控状态。一张纸对折一次会变成 2 层,再对折一次会变成 4 层……如此下去,每对折一次这个数目便会翻一倍。
因此,一张纸对折了 n 次后,你就能得到 2n 层纸。当 n = 5 时,纸张层数 2n = 32;当 n = 10 时,纸张层数瞬间变成了 1024;当 n = 30 时,你面前将出现 230 = 1 073 741 824 层纸!一张纸的厚度大约是 0.1 毫米,这十亿多张纸叠加在一起,也就有 10 万多米。
卡门线(Kármán line)位于海拔 100 千米处,是国际标准规定的外太空与地球大气层的界线。这表明,把一张纸对折 30 次以后,其总高度将会超出地球的大气层,直达外太空。
波斯史诗《王书》记载的故事也形象地道出了指数级增长的猛烈程度。一位智者发明了国际象棋,国王想要奖赏他,问他想要什么。智者说:“在这个棋盘的第一个格子里放上一颗大米,第二个格子里放上两颗大米,第三个格子里放上四颗大米,以此类推,每个格子里的大米数都是前一个格子的两倍。所有 64 个格子里的大米就是我想要的奖赏了。”国王觉得这很容易办到,便欣然同意了。
殊不知,哪怕只看第 64 个格子里的大米,就已经有 263 ≈ 9.22 × 1019 颗了。如果把这些大米分给当时世界上的每个人,那么每一个人都会得到上千吨大米。国际象棋的棋盘里幸好只有 64 个格子。如果国际象棋的棋盘里有 300 个格子,里面的大米颗数就会超过全宇宙的原子总数了。
因而,在计算机算法领域,我们有一个最基本的假设:所有实用的、快速的、高效的算法,其时间复杂度都应该是多项式级别的。 因此,在为计算机编写程序解决实际问题时,我们往往希望算法的时间复杂度是多项式级别的。
这里的“问题”一词太过宽泛,可能会带来很多麻烦,因而我们规定,接下来所说的问题都是指的“判定性问题”(decision problem),即那些给定某些数据之后,要求回答“是”或者“否”的问题。
在复杂度理论中,如果某个判定性问题可以用计算机在多项式级别的时间内解出,我们就说这个问题是一个 P 问题,或者说它属于集合 P。这里,P 是“多项式”的英文单词 polynomial 的第一个字母。之前那个叠放东西的问题,就是一个 P 问题。
历史上至少有过两个问题,它们看起来非常困难,非常不像 P 问题,但在人们的不懈努力之下,最终还是成功地加入了 P 问题的大家庭。其中一个是线性规划(linear programming),它是一种起源于二战时期的运筹学模型。
1947 年,乔治·丹齐格(George Dantzig)提出了一种非常漂亮的算法叫作“单纯形法”(simplex algorithm),它在随机数据中的表现极为不错,但在最坏情况下却需要耗费指数级的时间。因此,很长一段时间,人们都在怀疑,线性规划是否有多项式级的算法。直到 1979 年,人们才迎来了线性规划的第一个多项式级的算法,它是由前苏联数学家列昂尼德·哈奇扬(Leonid Khachiyan)提出的。
另外一个问题则是质数判定问题(primality test):判断一个正整数是否是质数(prime),或者说判断一个正整数是不是无法分成两个更小的正整数之积。人们曾经提出过各种质数判定的多项式级算法,但它们要么是基于概率的,要么是基于某些假设的,要么是有一定适用范围的。
2002 年,来自印度理工学院坎普尔分校的阿格拉瓦尔(M. Agrawal)、卡亚勒(N. Kayal)和萨克斯泰纳(N. Saxena)发表了一篇重要的论文《PRIMES is in P》,给出了第一个确定性的、时间复杂度为多项式级别的质数判定算法,质数判定问题便也归入了 P 问题的集合。
同时,我们也有很多游离于集合 P 之外的问题。互联网安全高度依赖于一种叫作 RSA 算法的加密体系,里面用到了非常犀利的一点:在整数世界里,合成与分解的难度是不对等的。
任意选两个比较大的质数,比如 19 394 489 和 27 687 937。我们能够很容易计算出它俩相乘的结果,它等于 536 993 389 579 193;但是,如果反过来问你,536 993 389 579 193 可以分解成哪两个质数的乘积,这却非常难以迅速作答。把一个大整数分解成若干个质数之积,这就是著名的“整数分解问题”(integer factorization problem)。
目前,人们还没有找到一种快速有效的整数分解算法。也就是说,目前人们还不知道整数分解问题是否属于 P。(这里我们指的也是整数分解问题的判定性版本,即给定一个正整数 N 和一个小于 N 的正整数 M,判断出 N 是否能被某个不超过 M 的数整除。)人们猜测,整数分解很可能不属于 P。这正是 RSA 算法目前足够安全的原因。
另一个著名的问题叫作“子集和问题”(subset sum problem):给定一个整数集合 S 以及一个大整数 M,判断出能否在 S 里选出一些数,使得它们的和正好为 M?比方说,假设集合 S 为
{38, 71, 45, 86, 68, 65, 82, 89, 84, 85, 91, 8}
并且大整数 M = 277,那么你就需要判断出,能否在上面这一行数里选出若干个数,使得它们相加之后正好等于 277。为了解决这类问题,其中一种算法就是,枚举所有可能的选数方案,看看有没有满足要求的方案。
如果我们用 n 来表示集合里的元素个数,那么所有可能的选数方案就有 O(2n) 种,检验每一种方案都需要花费 O(n) 的时间,因而整个算法的时间复杂度为 O(n · 2n)。虽然人们已经找到了时间复杂度更低的算法,但没有一种算法的时间复杂度是多项式级别的。人们猜测,子集和问题很可能也不属于 P。
美国计算机科学家杰克·埃德蒙兹(Jack Edmonds)在 1964 年的一篇讨论某个矩阵问题的论文中,也提到了类似于 P 问题的概念:“当然,给定一个矩阵后,考虑所有可能的染色方案,我们一定能碰上一个符合要求的剖分,但这种方法所需要的工作量大得惊人。
我们要寻找一种算法,使得随着矩阵大小的增加,工作量仅仅是呈代数式地上涨……和大多数组合问题一样,找出一个有限的算法很容易,找出一个满足上述条件的,从而能在实际中运用的算法,就不那么容易了。”
接下来,埃德蒙兹模模糊糊地触碰到了一个新的概念:“给定一个矩阵,它的各列最少能被剖分成多少个独立集?我们试着找出一个好的刻画方式。至于什么叫作‘好的刻画’,我们则采用‘绝对主管原则’。一个好的刻画,应该能透露出矩阵的某些信息,使得某个主管能够在助手找到一个最小的剖分方案之后,轻易地验证出这确实是最小的剖分方案。
有了一个好的刻画,并不意味着就有一个好的算法。助手很可能还是得拼死拼活,才能找到那个剖分方案。”
埃德蒙兹后面所说的,不是设计一种多项式级的算法来寻找答案,而是设计一种多项式级的算法来验证答案的正确性。对于很多问题,这件事情是很好办的。为了向人们展示出确实有可能让所有的物体都不被压坏,我们只需要给出一种满足要求的物体叠放顺序,并让计算机用 O(n) 的时间验证它的确满足要求即可。为了向人们展示出集合中的某些数加起来能得出 277,我们只需要提供一种选数的方法,并让计算机用 O(n) 的时间求和检验。
对于有些问题来说,如果答案是肯定的,我们可能并没有一种非常明显的高效方法来检验这一点。不过,很容易看出,找出一个多项式级的答案验核算法,再怎么也比找出一个多项式级的答案获取算法更容易。很多看上去非常困难的问题,都是先找到多项式级的答案验核算法,再找到多项式级的答案获取算法的。
一个经典的例子就是质数判定问题。如果某个数确实是一个质数,你怎样才能在多项式级的时间里证明这一点?1975 年,沃恩·普拉特(Vaughan Pratt)在《每个质数都有一份简短的证明书》(Every Prime Has a Succinct Certificate)一文中给出了一种这样的方法,无疑推动了质数判定算法的发展。
还有些问题是如此之难,以至于目前人们不但没有找到多项式级的答案获取算法,而且还不知道是否存在多项式级的答案验核算法。
比如经典的“第 K 大子集问题”(Kth largest subset problem):给定一个含有 n 个整数的集合 S,一个大整数 M,以及一个不超过 2n 的整数 K,判断出是否存在至少 K 个不同的子集,使得每个子集里的元素之和都不超过 M?
如果答案是肯定的,一个很容易想到的验证方法便是,把所有满足要求的 K 个子集都列出来,并交由计算机审核。只可惜,子集的数目是指数级的,因而审核工作也将会花费指数级的时间。人们猜测,第 K 大子集问题很可能没有多项式级别的检验方法。
在复杂度理论中,一个问题有没有高效的答案验核算法,也是一个非常重要的研究课题。对于一个判定性问题,如果存在一个多项式级的算法,使得每次遇到答案应为“是”的时候,我们都能向这个算法输入一段适当的“证据”,让算法运行完毕后就能确信答案确实为“是”,我们就说这个问题是一个 NP 问题,或者说它属于集合 NP。为了解释“NP 问题”这个名字的来由,我们不得不提到 NP 问题的另一个等价定义:可以在具备随机功能的机器上用多项式级的时间解决的问题。
如果允许计算机的指令发生冲突,比如指令集里面既有 “如果遇到情况 A,则执行操作 B”,又有 “如果遇到情况 A,则执行操作 C”,我们就认为这样的计算机具备了随机的功能。这种新型的计算机就叫作“非确定型”(nondeterministic)机器。
机器一旦遇到了矛盾纠结之处,就随机选择一条指令执行。你可以把机器面对的每一次随机选择都想象成是一个通向各个平行世界的岔路口,因而整台机器可以同时试遍所有的分支,自动探寻所有的可能。
如果你看过尼古拉斯·凯奇(Nicolas Cage)主演的电影《预见未来》(Next),你或许会对这一幕非常熟悉。只要在任意一个分支里机器回答了“是”,那么整台机器也就算作回答了“是”。
在如此强大的机器上,很多问题都不是问题了。为了判断出能否让所有的物体都不被压坏,我们只需要让机器每次都从剩余物体中随便选一个放,看看由此产生的 n! 种放法里是否有哪种放法符合要求。为了判断出集合中是否有某些数加起来等于 277,我们只需要让机器随机决定每个数该选还是不选,最后看看有没有哪次选出来的数之和正好是 277。
事实上,在非确定型计算机上可以用多项式级的时间获取到答案的问题,正是那些在确定型计算机上可以用多项式级的时间验核答案的问题,原因很简单:如果一个问题可以在非确定型计算机上获解,找到解的那个分支沿途做出的选择就成了展示答案正确性的最有力证据;反之,如果我们能在确定型计算机上验核出答案确实为“是”,我们便可以在非确定型计算机上随机产生验核所需的证据,看看在所有可能的证据当中会不会出现一条真的能通过验核的证据。
“非确定型”的英文单词是 nondeterministic,它的第一个字母是 N;“多项式”的英文单词是 polynomial,它的第一个字母是 P。NP 问题便如此得名。
容易想到,所有的 P 问题一定都是 NP 问题,但反过来就不好说了。例如,子集和问题是属于 NP 的。然而,之前我们就曾经讨论过,人们不但没有找到子集和问题的多项式级解法,而且也相信子集和问题恐怕根本就没有多项式级的解法。因而,子集和问题很可能属于这么一种类型的问题:它属于集合 NP,却不属于集合 P。
1971 年,史提芬·古克(Stephen Cook)发表了计算机科学领域最重要的论文之一——《定理证明过程的复杂性》(The Complexity of Theorem-Proving Procedures)。在这篇论文里,史提芬·古克提出了一个著名的问题:P 等于 NP 吗?
如果非要用一句最简单、最直观的话来描述这个问题,那就是:能高效地检验解的正确性,是否就意味着能高效地找出一个解?数十年来,无数的学者向这个问题发起了无数次进攻。根据格哈德·韦金格(Gerhard Woeginger)的统计,仅从 1996 年算起,就有 100 余人声称解决了这个问题,其中 55 人声称 P 是等于 NP 的,另外 45 人声称 P 是不等于 NP 的,还有若干人声称这个问题理论上不可能被解决。
但不出所料的是,所有这些“证明”都是错误的。目前为止,既没有人真正地证明了 P = NP,也没有人真正地证明了 P ≠ NP,也没有人真正地证明了这个问题的不可解性。这个问题毫无疑问地成为了计算机科学领域最大的未解之谜。
在 2000 年美国克雷数学研究所(Clay Mathematics Institute)公布的千禧年七大数学难题(Millennium Prize Problems)中,P 和 NP 问题排在了第一位。第一个解决该问题的人将会获得一百万美元的奖金。
让我们来看一下,科学家们都是怎么看 P 和 NP 问题的吧。英国数学家、生命游戏(Game of Life)的发明者约翰·康威(John Conway)认为,P 是不等于 NP 的,并且到了 21 世纪 30 年代就会有人证明这一点。他说道:“我觉得这本来不应该是什么难题,只是这个理论来得太迟,我们还没有弄出任何解决问题的工具。”
美国计算机科学家、1985 年图灵奖获得者理查德·卡普(Richard Karp)也认为,P 是不等于 NP 的。他说:“我认为传统的证明方法是远远不够的,解决这个问题需要一种绝对新奇的手段。直觉告诉我,这个问题最终会由一位不被传统思想束缚的年轻科学家解决掉。”
美国计算机科学家、《自动机理论、语言和计算导论》(Introduction to Automata Theory, Languages and Computation)的作者杰夫瑞·厄尔曼(Jeffrey Ullman)同样相信 P 不等于 NP。他说:“我认为这个问题和那些困扰人类上百年的数学难题有得一拼,比如四色定理(four color theorem)。
所以我猜测,解决这个问题至少还要 100 年。我敢肯定,解决问题所需的工具至今仍未出现,甚至连这种工具的名字都还没有出现。但别忘了,那些最伟大的数学难题刚被提出来的 30 年里,所面对的也是这样的情况。”
你或许会注意到,大家似乎都倾向于认为 P ≠ NP 。事实上,根据威廉·加萨奇(William Gasarch)的调查,超过八成的学者都认为 P ≠ NP。这至少有两个主要的原因。首先,证明 P = NP 看上去比证明 P ≠ NP 更容易,但即使这样,目前仍然没有任何迹象表明 P = NP。
为了证明 P = NP,我们只需要构造一种可以适用于一切 NP 问题的超级万能的多项式级求解算法。在那篇划时代的论文里,史提芬·古克证明了一个颇有些出人意料的结论,让 P = NP 的构造性证明看起来更加唾手可得。给你一堆正整数,问能否把它们分成总和相等的两堆,这个问题叫作“分区问题”(partition problem)。
容易看出,分区问题可以转化为子集和问题的一个特例,你只需要把子集和问题中的目标设定成所有数之和的一半即可。这说明,子集和问题是一个比分区问题更一般的“大问题”,它可以用来解决包括分区问题在内的很多“小问题”。
史提芬·古克则证明了,在 NP 问题的集合里,存在至少一个最“大”的问题,它的表达能力如此之强,以至于一切 NP 问题都可以在多项式的时间里变成这个问题的一种特例。
很容易想到,如果这样的“终极 NP 问题”有了多项式级的求解算法,所有的 NP 问题都将拥有多项式级的求解算法。这样的问题就叫作“NP 完全问题”(NP-complete problem)。在论文中,史提芬·古克构造出了一个具体的 NP 完全问题,它涉及到了很多计算机底层的逻辑运算,能蕴含所有的 NP 问题其实也不是非常奇怪的事。
后来,人们还找到了很多其他的 NP 完全问题。1972 年,理查德·卡普发表了《组合问题中的可归约性》(Reducibility among Combinatorial Problems)一文。这是复杂度理论当中又一篇里程碑式的论文,“P 问题”、“NP 问题”、“NP 完全问题”等术语就在这里诞生。
在这篇论文里,理查德·卡普列出了 21 个 NP 完全问题,其中不乏一些看起来很“正常”、很“自然”的问题,刚才提到的子集和问题就是其中之一。
1979 年,迈克尔·加里(Michael Garey)和戴维·约翰逊(David Johnson)合作出版了第一本与 NP 完全问题理论相关的教材——《计算机和难解性:NP 完全性理论导引》(Computers and Intractability: A Guide to the Theory of NP-Completeness)。该书的附录中列出了超过 300 个 NP 完全问题,这一共用去了 100 页的篇幅,几乎占了整本书的三分之一。
如果这些 NP 完全问题当中的任何一个问题拥有了多项式级的求解算法,所有的 NP 问题都将自动地获得多项式级的求解算法,P 也就等于 NP 了。然而,这么多年过去了,没有任何人找到任何一个 NP 完全问题的任何一种多项式解法。这让人们不得不转而相信,P 是不等于 NP 的。
人们相信 P ≠ NP 的另一个原因是,这个假设经受住了实践的考验。工业与生活中的诸多方面都依赖于 P ≠ NP 的假设。如果哪一天科学家们证明了 P = NP,寻找一个解和验证一个解变得同样容易,这个世界将会大不一样。1995 年,鲁塞尔·因帕利亚佐(Russell Impagliazzo)对此做了一番生动描述。
首先,各种各样的 NP 问题,尤其是那些最为困难的 NP 完全问题,都将全部获得多项式级的解法。工业上、管理上的几乎所有最优化问题都立即有了高效的求解方案。事实上,我们甚至不需要编程告诉计算机应该怎样求解问题,我们只需要编程告诉计算机我们想要什么样的解,编译器将会自动为我们做好一个高效的求解系统。
其次,很多人工智能问题也迎刃而解了。比方说,为了让计算机具备中文处理能力,我们可以准备一个训练集,里面包含一大批句子样本,每个句子都带有“符合语法”、“不符合语法”这两种标记之一。
接下来,我们要求计算机构造一个代码长度最短的程序,使得将这些语句输入这个程序后,程序能正确得出它们是否符合语法。显然,这个最优化问题本身是一个 NP 问题(这里有个前提,即这样的程序是存在的,并且是多项式级别的),因此计算机可以在多项式时间内找到这个最简程序。
根据奥卡姆剃刀原理(Occam’s razor),我们有理由相信,这个程序背后的算法也就是人类头脑中正在使用的算法,因此它能够适用于所给材料之外的其他语句,并具有自我学习的功能。
数学家的很多工作也可以完全交给计算机来处理。寻找一个反例和验证一个反例变得同样简单,各种错误的猜想都将很快被推翻。事实上,寻找一个数学证明和验证一个证明的正确性也变得同样简单,因此各种正确的命题也能够很快找到一个最简的证明。
最后,不要高兴得太早——P = NP 的世界也将会是一个极不安全的世界。电子签名技术不再有效,因为伪造一段合法的签名变得和验证签名是否合法一样轻松。RSA 算法也不再有效,因为寻找一个质因数变得和判断整除性一样简单。事实上,发明任何新的密码算法都是徒劳——计算机可以根据一大批明文密文样本推算出生成密文的算法(只要这个算法本身是多项式的)。
更进一步,在网络上,你再也没法把人和人区别开来,甚至没法把人和计算机区别开来。计算机不仅能轻易通过图灵测试(Turing test),还能精确地模仿某一个特定的人。
如果你能把某个人的网络聊天记录全部搜集起来,把这个人和网友们的对话全部递交给计算机,计算机将会很快学会如何模仿这个人。网络的身份鉴定必须要借助物理手段。即使是在科幻故事中,这样的设定也相当疯狂,可见 P = NP 有多不可能了。
虽然种种证据表明 P ≠ NP,但我们仍然无法排除 P = NP 的可能性。其实,如果 P 真的等于 NP,但时间复杂度的次数非常大非常大非常大,密码学的根基仍然不太可能动摇,我们的世界仍然不太可能大变。被誉为“算法分析之父”的计算机科学大师高德纳(Donald Knuth)还提出了这样一种可能:未来有人利用反证法证明了 P = NP,于是我们知道了所有 NP 问题都有多项式级的算法,但算法的时间复杂度究竟是多少,我们仍然一无所知!
对于很多人来说,找不到任何一个 NP 完全问题的多项式级算法,同样不应成为质疑 P = NP 的理由。荻原光德(Mitsunori Ogihara)认为,最终人们或许会成功地证明 P = NP,但这绝不是一两个人死死纠缠某一个 NP 完全问题就能办到的。对此,他做了更为细致的想象。
XX 世纪后期,一份非常简略的、从未发表过的草稿,无意中开辟了解决 P 和 NP 问题的道路。这份草稿出自 20 世纪的一位数学天才 FOO 之手,当时他正在尝试着建立某种代数结构的新理论。显然,FOO 很快放弃了这个想法,并且今后从未重新拾起这个课题。这份草稿一直卡在 FOO 的卧室地板的缝隙里,在后来的一次旧房翻新工程中才被工人们发现。
由于草稿太过简略,因而当时并未引起太多关注。然而,几十年后,一群数学家发现,如果草稿上面的某个假设的某个变形成立,将会推出很多有意思的东西。虽然这不是 FOO 本来要做的假设,但它还是被人们称作“FOO 假设”,以纪念这位数学天才。
大约 100 年后,一群计算机科学家发现,如果 FOO 假设成立,那么某个特定的代数问题 Q 将会成为一个 NP 完全问题。几年后,计算机科学家们再次发现,如果(届时已经非常有名的)BAR 猜想成立,那么 Q 将会拥有多项式级的算法。把两者结合起来,于是得到:如果 FOO 和 BAR 都成立,那么 P = NP。
接下来的两个世纪里,这两个猜想都有了相当充分的研究。人们不断地得出各式各样的部分结果,剩余的特例则被转化为新的形式,直至每个猜想都被归为一句非常简明、非常具体的命题。最终,两组人马相继宣布,这两个命题都是正确的。第一组人马在 FOO 的诞辰前三周宣布,他们终于攻克了 BAR 猜想的最后一环。三个月后,第二组人马宣布,FOO 猜想正式得以解决。
未来究竟会发生什么?让我们拭目以待。